The AES Key Schedule explained

I recently started the cryptopals challenge and had to re-study how AES works to implement it in Go. I decided to publish my notes on the AES algorithm to help my future self and anyone here get started or get re-acquainted with the cryptographic standard.

This article is not a copy-paste of the AES specification. I wanted to write an introduction that helps the reader understand the basics of the AES key schedule. At the end of this article you should know enough to read the actual AES specification with ease and implement the key schedule yourself.

If you're interested in seeing an implementation close to the specification, checkout the one I coded for the cryptopals challenge. For a real world implementation I recommend Go's aes crypto package.

AES in summary

Let's start with a quick recap. The Advanced Encryption Standard is a symmetric cipher, which means that you need a secret key to encrypt a plaintext and the same key to decrypt the ciphertext. The key can be 128, 192 or 256 bits. In the rest of this article I assume that we are working with AES-128 that uses a key of 128 bits.

But AES is also a block cipher, which means that it encrypts blocks of 128 bits in multiple rounds before outputting the final ciphertext.

Since there are multiple rounds of encryption for one block, do we use the same key every time ?

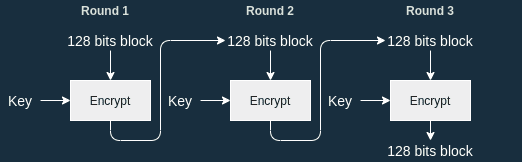
No we don't do that because it would expose us to slide attacks: a cryptanalysis technique relying on the fact that we use the same key every round.

Key Expansion

To avoid using the same key every round, we derive new keys (called Round Keys) from the original one. This is called a key schedule:

A key schedule is an algorithm that calculates all the round keys from the key.

In this article I will use the same notation found in the original specification. Let's start by defining some constants. We write:

$K$ the cipher key. It is 128 bits long.
$N_k$ the number of 32-bit words comprising the cipher key. Here $N_k = 4$ .
$N_r$ the number of rounds. Here $N_r = 10$ .
$N_b$ the number of columns comprising the State (basically the number of 32-bit words comprising a block). $N_b = 4$ .

Since there are 10 rounds, we have to produce 10 round keys. Each round key is then used in the corresponding round:

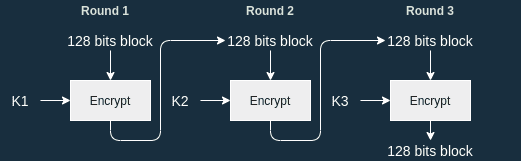
AES Key schedule

The AES key schedule generates a total of 11 subkeys $[K_0, K_1, ..., K_{10}]$ of 128 bits each (even in AES-192 and AES-256).

11 subkeys? But there are only 10 rounds !

That's because first key $K_0$ is XOR'd with the plaintext before the first round. Check out my post explaining AES for more info.

The operations are done on 32-bit words so we adapt our notation to work with this: the result of the key schedule is an array of 32-bit words denoted $[w_i]$ , where $0 \le i \lt 11$ .

Consider the cipher key $K$ composed of 128 bits. We split the key in 32-bit words denoted $w_i$ :

K = [ w_0, w_1, w_2, w_3 ]

See how I used the notation $w_i$ ? This is because the cipher key $K$ is actually the first round key : $K_0 = K$ .

$K_0 = K$ is only applicable for AES-128.

Then each new subkey depends on the previous subkey. To compute $K_1 = [w_4, w_5, w_6, w_7]$ the algorithm is the following:

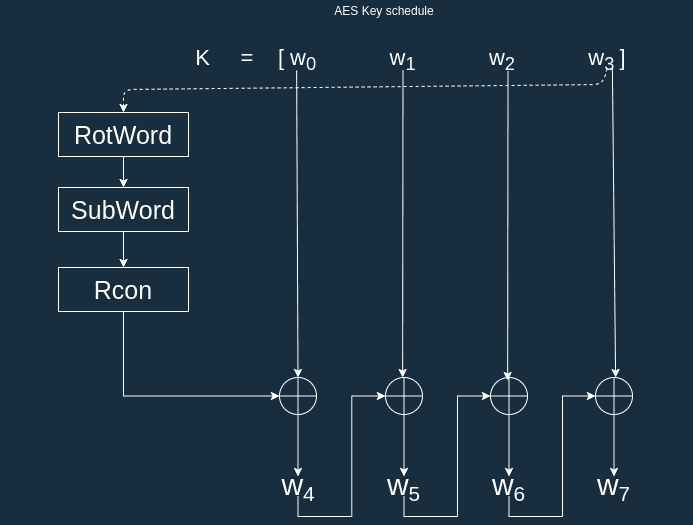
The general rule is that:

w_i = w_{i-N_k} \oplus w_{i-1}

For instance $w_6 = w_{6 - 4} \oplus w_5 = w_2 \oplus w_5$ .

The exception occurs when we have to compute a new $w_i$ and $i \equiv 0 \pmod{N_k}$ . Here we want to compute $w_4$ and $4 \equiv 0 \pmod 4$ . In this case, the previous word $w_3$ undergoes some transformation with the functions RotWord, SubWord and Rcon (more on this later).

To compute $K_2 = [w_8, w_9, w_{10}, w_{11}]$ , we apply the same algorithm to $K_1 = [w_4, w_5, w_6, w_7]$ . In total this is repeated 10 times.

Independently of the size of the cipher key you are using (AES-128, AES-192 or AES-256), the length of the Round Key is always the size of the state. In other words, the size of the Round Key is the size of a block.

RotWord

RotWord is quite simple. It takes a 4-byte word $[a_0, a_1, a_2, a_3]$ and returns $[a_1, a_2, a_3, a_0]$ .

Here each $a_i$ is a byte composed of 8 bits.

SubWord

SubWord is a little bit more complex. It takes a 4-byte word $[a_0, a_1, a_2, a_3]$ and applies the AES S-Box to each of the bytes to produce a new 4-byte word $[b_0, b_1, b_2, b_3]$ .

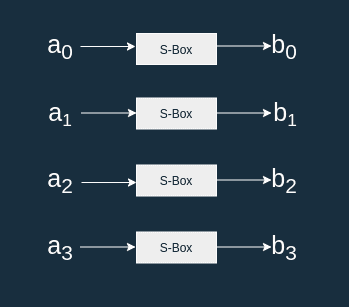
S-box

The S-box is a substitution table also used in the encryption algorithm. Think of it as a big lookup table that maps an 8-bit input to an 8-bit output. For instance b3 is mapped to 6d.

For an input $c$ there is a way to compute the output $s = S(c)$ . You start by computing the multiplicative inverse of $c$ in $GF(2^8)$ , we name it $b = [b_0, b_1, b_2, b_3, b_4, b_5, b_6, b_7]$ .

Then you can compute $s$ using the affine transformation - source wikipedia:

\begin{bmatrix}s_0\\s_1\\s_2\\s_3\\s_4\\s_5\\s_6\\s_7\end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \\ 1 & 1 & 0 & 0 & 0 & 1 & 1 & 1 \\ 1 & 1 & 1 & 0 & 0 & 0 & 1 & 1 \\ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 1 \\ 1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & 1 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 \end{bmatrix}\begin{bmatrix} b_0\\ b_1\\ b_2\\ b_3\\ b_4\\ b_5\\ b_6\\ b_7 \end{bmatrix} + \begin{bmatrix} 1 \\ 1\\ 0\\ 0\\ 0\\ 1\\ 1\\ 0 \end{bmatrix}

In practice, it's easier to implement the S-box as a constant lookup table. I give some complementary information in my post about the AES algorithm.

Rcon

Rcon is a round constant word array. For each round, you get 4-byte word. For your convenience here are the values of $rcon[i]$ noted as $rc_i$ , in hexadecimal:

i	1	2	3	4	5	6	7	8	9	10
$rc_i$	01	02	04	08	10	20	40	80	1B	36

The computation of $rc_i$ involves a lot of algebra. Basically $rc_{i} = x^{i-1}$ . Where $x$ is 02 in hexadecimal, and the multiplication is done is the finite field $GF(2^8)$ .

Conclusion

This is it, you now know enough to implement the AES key schedule on your own (with the official specification as a reference of course). One last thing, you might not have noticed that an attacker who managed to retrieve a round key $K_i$ , is able to determine all the other round keys as well as the cipher key $K$ by reversing the algorithm. An attacker could retrieve a round key thanks to a side channel attack.

I wrote two other posts about AES:

the first one describes the encryption algorithm
the seconde one describes the decryption algorithm

Resources

I used and studied the following resources while writing this article:

On this page