The AES encryption algorithm explained

This article is not a copy-paste of the AES specification. I wanted to write an introduction that helps the reader understand the basics of the AES algorithm. To read this article you should have at least some vague knowledge of what encryption is and you should be comfortable with words like bits, bytes and XOR. At the end of this article you should know enough to read the actual AES specification with ease and implement the encryption algorithm yourself. To keep the article short I focus only on the encryption algorithm.

If you're interested in seeing an implementation close to the specification, checkout the one I coded for the cryptopals challenge. For a real world implementation I recommend Go's aes crypto package.

AES in summary

Let's start with a quick recap. The Advanced Encryption Standard is a symmetric cipher, which means that you need a secret key to encrypt a plaintext and the same key to decrypt the ciphertext. The key can be 128, 192 or 256 bits. In the rest of this article I assume that we are working with AES-128 that uses a key of 128 bits.

But AES is also a block cipher, which means that it encrypts inputs of 128 bits in multiple rounds before outputting the final output: a 128-bit ciphertext. Each round gets a different key called round key. The round keys are derived from the cipher key. Take a look at my previous post for more information about round keys and how they are generated.

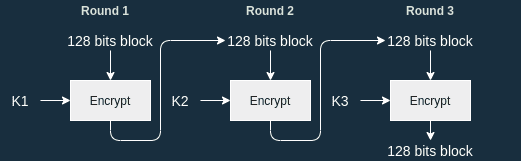
Encryption algorithm overview

$K$ is our cipher key and $[K_0, K_1, ..., K_{10}]$ are the round keys derived from $K$ .
$P$ is a 128-bit block that we want to encrypt: our plaintext.
$C$ is the ciphertext: the result of encrypting $P$ with AES and $K$ . This is also a 128-bit block.

We need a 128-bit plaintext because AES is a block cipher. The only thing it can do is encrypt blocks. To do so the block goes through a series of rounds. Each round performs some substitutions and permutations.

AES is a substitution-permutation network, the substition is provided by SubBytes and the permutation by ShiftRows and MixColumns.

With AES-128 we have 10 rounds:

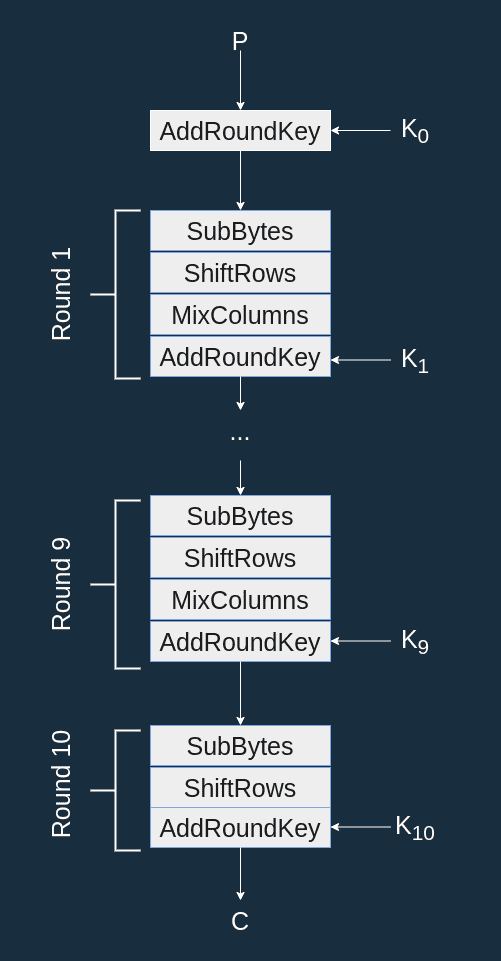
The AES state is the current value of the bytes being encrypted (more on this later). After the first AddRoundKey the state is equal to $P \oplus K_0$ .

Each round is made up of 4 functions:

SubBytes: a substitution (or mapping) based on the AES S-box.
ShiftRows: applies some rotations on the state.
MixColumns: divides the state in multiple words and mix them together.
AddRoundKey: XORs a round key to the state.

Before the first round, the plaintext is XOR'd to $K_0$ . The last round does not apply MixColumns since it has no security relevance (more on that later).

AES State

The AES state is the array of bytes on which the cryptographic operations are being performed. At the very beginning of the algorithm, the state is equal to the 128-bit plaintext block. At the end of the algorithm, it is equal to the ciphertext.

The state is often represented as a matrix. Let $p_0, p_1, ..., p_{15}$ the 16 bytes of the plaintext $P$ . Then we represent the state as $s_{0,0}, s_{0,1}, ..., s_{3,3}$ :

\begin{bmatrix} p_0 & p_4 & p_8 & p_{12} \\ p_1 & p_5 & p_9 & p_{13} \\ p_2 & p_6 & p_{10} & p_{14} \\ p_3 & p_7 & p_{11} & p_{15} \\ \end{bmatrix} \to \begin{bmatrix} s_{0,0} & s_{0,1} & s_{0,2} & s_{0,3} \\ s_{1,0} & s_{1,1} & s_{1,2} & s_{1,3} \\ s_{2,0} & s_{2,1} & s_{2,2} & s_{2,3} \\ s_{3,0} & s_{3,1} & s_{3,2} & s_{3,3} \\ \end{bmatrix}

We note $N_b$ the number of columns comprising the state. $N_b = 4$ . The state is always 128 bits independently of the key length.

SubBytes

SubBytes applies the S-box to each byte of the state (see below).

S-box

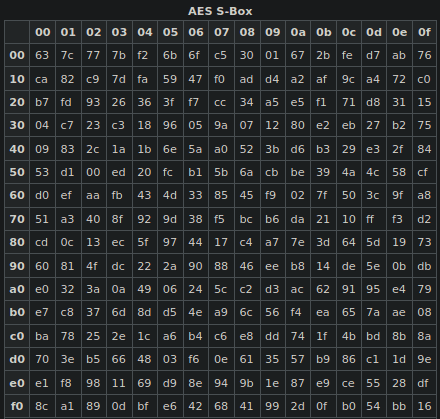
The AES S-box is a lookup table that maps a byte to another byte. For instance b3 is mapped to 6d.

Computing the S-box

Let $a$ be a byte, to compute the mapping $s = S(a)$ :

Compute the multiplicative inverse of $c$ in $GF(2^8)$ , we name it $b = [b_0, b_1, b_2, b_3, b_4, b_5, b_6, b_7]$ .
Apply the following affine transformation:

s_i = b_i \oplus b_{(i+4) \mod 8} \oplus b_{(i+5) \mod 8} \oplus b_{(i+6) \mod 8} \oplus b_{(i+7) \mod 8} \oplus c_i

Where $c_i$ is the $i^{th}$ bit of {01100011}.

S-box table

There are other ways to compute the mapping. You can use a matrix form, or you can use a precomputed lookup table. The latter is probably the most convenient, here is the S-box in all its glory (taken from Wikipedia):

ShiftRows

ShiftRows performs a cyclical rotation of the bytes of the state by rows:

The first row is not shifted.
The second row is shifted left by 1 byte.
The third row is shifted left by 2 bytes.
The fourth row is shifted left by 3 bytes.

\begin{bmatrix} s_{0,0} & s_{0,1} & s_{0,2} & s_{0,3} \\ s_{1,0} & s_{1,1} & s_{1,2} & s_{1,3} \\ s_{2,0} & s_{2,1} & s_{2,2} & s_{2,3} \\ s_{3,0} & s_{3,1} & s_{3,2} & s_{3,3} \\ \end{bmatrix} \to \begin{bmatrix} s_{0,0} & s_{0,1} & s_{0,2} & s_{0,3} \\ s_{1,1} & s_{1,2} & s_{1,3} & s_{1,0} \\ s_{2,2} & s_{2,3} & s_{2,0} & s_{2,1} \\ s_{3,3} & s_{3,0} & s_{3,1} & s_{3,2} \\ \end{bmatrix}

MixColumns

MixColumns applies a transformation on each column of the state. Let $s_{i,i}$ be the bytes of the state as described earlier and $t_{i,i}$ the bytes of the state after the MixColumns transformation. For the column $0$ we have:

\begin{bmatrix} t_{0,0} \\ t_{1,0} \\ t_{2,0} \\ t_{3,0} \\ \end{bmatrix} = \begin{bmatrix} 02 & 03 & 01 & 01 \\ 01 & 02 & 03 & 01 \\ 01 & 01 & 02 & 03 \\ 03 & 01 & 01 & 02 \\ \end{bmatrix} \begin{bmatrix} s_{0,0} \\ s_{1,0} \\ s_{2,0} \\ s_{3,0} \\ \end{bmatrix}

MixColumns is a Hill cipher.

AddRoundKey

AddRoundKey computes a bitwise XOR between the state and the round key.

Remember: the size of a Round Key is always the size of the state.

Since operations are done on 4-byte (i.e. 32-bit) words let's split the round key in 4-byte words ( $i$ is the round number):

K_i = [w_{i*N_b}, w_{i*N_b + 1}, w_{i*N_b + 2}, w_{i*N_b + 3}]

We have seen that $N_b$ is the number of columns comprising the state, so $N_b = 4$ . Then, $K_1 = [w_4, w_5, w_6, w_7]$ . And as a reminder the state can be represented as four columns, each column $c$ defined by $s_c = \begin{bmatrix} s_{0,c} \\ s_{1,c} \\ s_{2,c} \\ s_{3,c} \end{bmatrix}$ .

Here $w_i$ and $s_c$ are 4-byte words and $s_{0,c}$ is one byte.

The result $t$ of AddRoundKey is the bitwise XOR between the state and the round key $K_i$ where the 4-byte word $t_c$ is defined by:

t_c = s_c \oplus w_{i*Nb + c}

Confusion, diffusion

Claude Shannon identified two properties of a secure cipher:

confusion: each bit of the ciphertext should depend on the key in a way that the relationship between the ciphertext and the key stays hidden.
diffusion: the modification of one bit of the plaintext should affect approximately half of the plaintext bits.

The steps of AES are designed to add confusion and diffusion:

Obviously AddRoundKey adds some dependency on the key, and as such, some confusion.
Thanks to ShiftRows, a modification on one bit in one column of the state affects other columns of the state and with MixColumns changing one byte of the state affects other bytes of the state. These two steps add diffusion.
SubBytes adds nonlinearity and confusion. Without it, you could encrypt a bunch of plaintext, get the corresponding ciphertexts and use a Gaussian elimination to retrieve the key.

Dispersion, conclusion

The designers of AES also defined a new term: dispersion. Here is their definition from their book The Design of Rijndael:

By dispersion we mean the operation by which bits or bytes that are close to each other in the context of θ are moved to positions that are distant.

Basically, dispersion means separating bits that are close together. This step is provided by ShiftRows.

This concludes this article, you should now have a fair understanding of how the AES encryptionalgorithm works if you ever need to code it or to break it. If you're interested in the decryption algorithm, go over to my next post.

Resources

I used and studied the following resources while writing this article:

On this page