The AES decryption algorithm explained

2020 August 11
Cryptography

In the previous article I explained how the encryption algorithm of AES is structured. This time I focus on the decryption algorithm. I'll use a lot of terms and functions defined in the previous post so if you don't understand something check it out. As usual the examples assume we are using AES-128.

If you're interested in seeing an implementation close to the specification, checkout the one I coded for the cryptopals challenge. For a real world implementation I recommend Go's aes crypto package.

The Inverse Cipher

To decrypt a ciphertext CC and produce a plaintext PP, the decryption algorithm uses the same round keys used in the encryption algorithm; however, the functions used in the encryption algorithm are reversed, we are now working with InvShiftRows, InvSubBytes and InvMixColumns.

Here is the decryption algorithm:

AES decryption algorithm

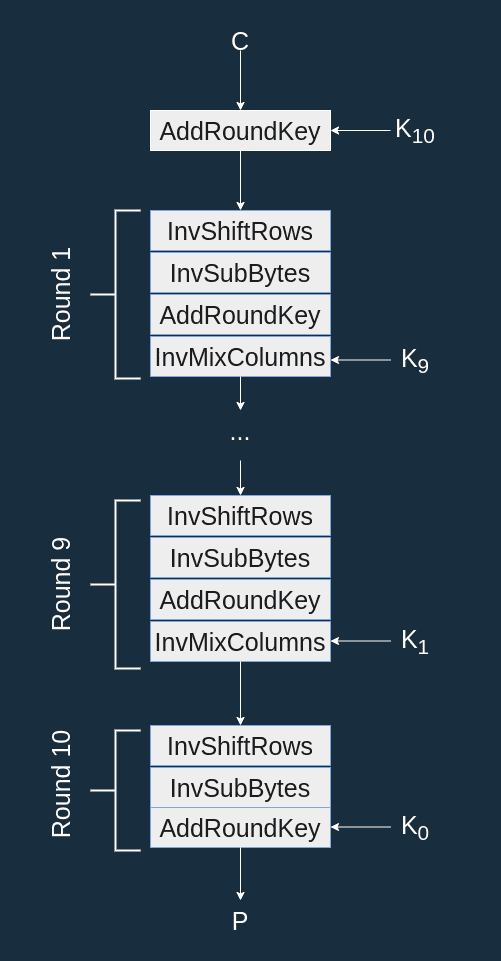
As we can see we don't just replace the transformations by their inverse, the order of the transformations are modified as well and we go through the round keys in reverse.

Inverse transformations

InvShiftRows

InvShiftRows performs the inverse cyclical rotation of ShiftRows (you shift right instead of left).

  1. The first row is not shifted.
  2. The second row is shifted right by 1 byte.
  3. The third row is shifted right by 2 bytes.
  4. The fourth row is shifted right by 3 bytes.
[s0,0s0,1s0,2s0,3s1,0s1,1s1,2s1,3s2,0s2,1s2,2s2,3s3,0s3,1s3,2s3,3]→[s0,0s0,1s0,2s0,3s1,3s1,0s1,1s1,2s2,2s2,3s2,0s2,1s3,1s3,2s3,3s3,0]\begin{bmatrix} s_{0,0} & s_{0,1} & s_{0,2} & s_{0,3} \\ s_{1,0} & s_{1,1} & s_{1,2} & s_{1,3} \\ s_{2,0} & s_{2,1} & s_{2,2} & s_{2,3} \\ s_{3,0} & s_{3,1} & s_{3,2} & s_{3,3} \\ \end{bmatrix} \to \begin{bmatrix} s_{0,0} & s_{0,1} & s_{0,2} & s_{0,3} \\ s_{1,3} & s_{1,0} & s_{1,1} & s_{1,2} \\ s_{2,2} & s_{2,3} & s_{2,0} & s_{2,1} \\ s_{3,1} & s_{3,2} & s_{3,3} & s_{3,0} \\ \end{bmatrix}

InvSubBytes

InvSubBytes applies the inverse S-box to each byte of the state. Here is the inverse S-box (from Wikipedia):

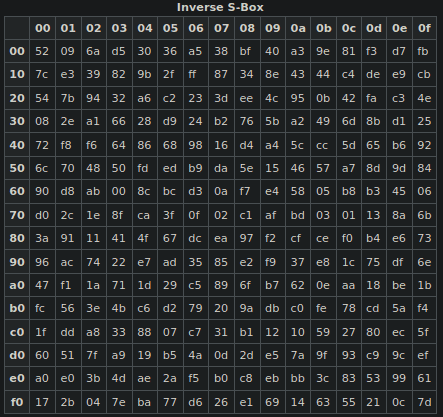
Inverse S-box

AddRoundKey

The inverse of a XOR is a XOR. So the inverse of AddRoundKey is AddRoundKey itself.

InvMixColumns

As with all other functions described here, InvMixColumns is the inverse of its counterpart MixColumns.

[t0,0t1,0t2,0t3,0]=[0e0b0d09090e0b0d0d090e0b0b0d090e][s0,0s1,0s2,0s3,0] \begin{bmatrix} t_{0,0} \\ t_{1,0} \\ t_{2,0} \\ t_{3,0} \\ \end{bmatrix} = \begin{bmatrix} 0e & 0b & 0d & 09 \\ 09 & 0e & 0b & 0d \\ 0d & 09 & 0e & 0b \\ 0b & 0d & 09 & 0e \\ \end{bmatrix} \begin{bmatrix} s_{0,0} \\ s_{1,0} \\ s_{2,0} \\ s_{3,0} \\ \end{bmatrix}

The Equivalent Inverse Cipher

The designers of AES also give another way of decrypting a block, using the same functions we just described. This alternative is based on several properties of the transformation but requires a small change in the key schedule.

New Round Keys

The round keys [K1,...,K9][K_1, ..., K_9] are transformed with InvMixColumns, I note DiD_i the new round keys:

Di=InvMixColumns(Ki)for1≤i<10 D_i = InvMixColumns(K_i) \quad \text{for} \quad 1 \le i \lt 10

The first and last round keys stay the same: D0=K0D_0 = K_0 and D10=K10D_{10} = K_{10}

You might be wondering how we are supposed to apply InvMixColumns on the key, since it usually applies on the state represented as a matrix. In the article describing the key schedule we wrote each round key KiK_i as an array of 4-byte words wcw_c:

K1=[w4,w5,w6,w7] K_1 = [w_4, w_5, w_6, w_7]

Each wcw_c is made up of 4 bytes and we can note each byte bk,cb_{k, c}:

wc=[b0,cb1,cb2,cb3,c] w_c = \begin{bmatrix} b_{0, c} \\ b_{1, c} \\ b_{2, c} \\ b_{3, c} \\ \end{bmatrix}

Then we can represent the key K1K_1 as matrix as well:

K1=[b0,4b0,5b0,6b0,7b1,4b1,5b1,6b1,7b2,4b2,5b2,6b2,7b3,4b3,5b3,6b3,7] K_1 = \begin{bmatrix} b_{0,4} & b_{0,5} & b_{0,6} & b_{0,7} \\ b_{1,4} & b_{1,5} & b_{1,6} & b_{1,7} \\ b_{2,4} & b_{2,5} & b_{2,6} & b_{2,7} \\ b_{3,4} & b_{3,5} & b_{3,6} & b_{3,7} \\ \end{bmatrix}

Schema

Thanks to this transformation we can now have an inverse cipher that looks just like the encryption cipher:

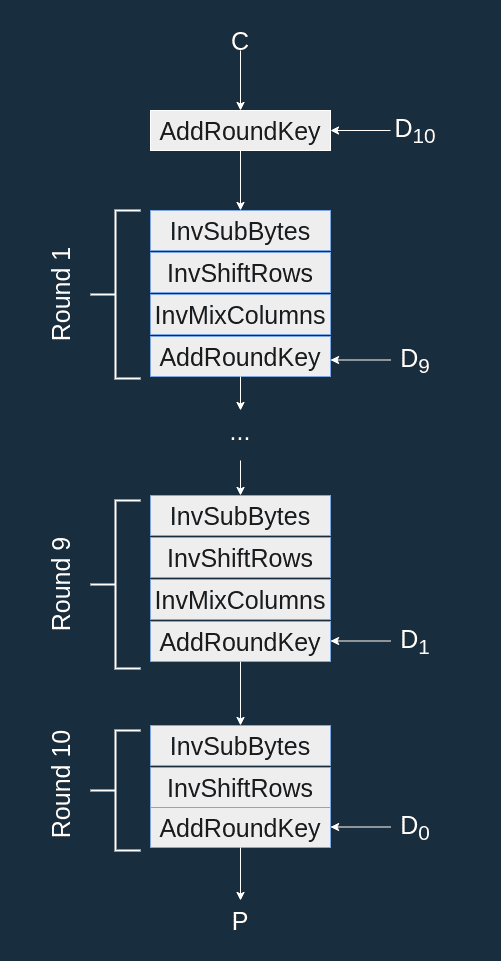
AES equivalent decryption algorithm

Notice how this is the encryption algorithm with the inverse transformations and the new round keys.

Conclusion

You should now have a fair understanding of the AES decryption algorithm. There is something I haven't mentionned yet, real life implementations of the encryption or decryption algorithm won't use the functions chained together:

   invMixColumns(invShiftRows(invSubBytes(state)))

Some implementations tricks will be used instead, check out Go's aes crypto package for an example. Here is their implementation of one decryption round:

for r := 0; r < nr; r++ {
    t0 = xk[k+0] ^ td0[uint8(s0>>24)] ^ td1[uint8(s3>>16)] ^ td2[uint8(s2>>8)] ^ td3[uint8(s1)]
    t1 = xk[k+1] ^ td0[uint8(s1>>24)] ^ td1[uint8(s0>>16)] ^ td2[uint8(s3>>8)] ^ td3[uint8(s2)]
    t2 = xk[k+2] ^ td0[uint8(s2>>24)] ^ td1[uint8(s1>>16)] ^ td2[uint8(s0>>8)] ^ td3[uint8(s3)]
    t3 = xk[k+3] ^ td0[uint8(s3>>24)] ^ td1[uint8(s2>>16)] ^ td2[uint8(s1>>8)] ^ td3[uint8(s0)]
    k += 4
    s0, s1, s2, s3 = t0, t1, t2, t3
}
Back to Blog