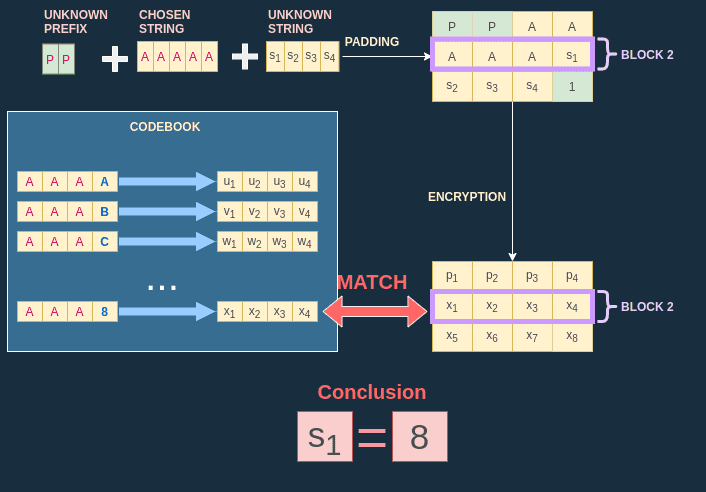
Cryptopals - ECB decryption (Harder)

Premises

In challenge 14 of the Cryptopals challenges I am given an oracle very similar to the one in Challenge 12. If you haven't read this post, I strongly advise you to do it now because I will build on this knowledge to tackle this new challenge.

The goal of the challenge is to decrypt a ciphertext encrypted with ECB. Obviously, I do not know the plaintext, but I am given an oracle to help me decrpyt the ciphertext. I call the plaintext unknown-string. The oracle works this way:

1. I have to give a message (i.e. a chosen string) to the oracle.
2. The oracle constructs a string by concatenating a prefix, my message and the unknown-string. The prefix is also an unknown string, but not our target.
3. The oracle encrypts the concatenated string with AES-128-ECB.

Oracle(message) = AES-128-ECB(prefix || message || unknown-string)

Battle plan

How should I approach this problem ? At first sight this problem looks rather similar to the challenge 12. The only difference is that there is now this prefix bothering me. If I manage to decrypt the prefix I can solve the problem just like challenge 12.

Anyway, here are some things that might be interesting to answer:

1. Can I find the block size ?
2. Can I find the prefix size ?
3. Can I decrypt the prefix ?

If I can answer these three questions, I have won. Actually to answer the first question I can apply exactly the same process I used in Challenge 12. So go check it out now if you haven't read it !

Gathering intel on the prefix size

Now that I have found the block size (16 bytes) I need to find the prefix size. For the purposes of the demonstration and to have readable diagrams, I will assume that:

• the block size is 4 bytes
• the message is always composed of the letter A and I note X the number of bytes in the message
• the prefix size is noted L

To understand how the prefix size is found, it is necessary to keep in mind some important and maybe obvious facts:

1. The prefix size will always constitute the first L bytes of the plaintext. Obvious enough isn't it ?
2. Each time I increase X (the length of our message), I "push" the unknown string a byte away.
3. ECB cuts out plaintext in blocks (of 4 bytes) and applies AES on each block independently. This has already been explained in previous blog posts. The important conclusion we can draw from this is that two ciphertexts blocks are equal if and only if the plaintext blocks are also equal.
4. By varying X and comparing the ciphertext blocks for each variation I can infer what part of the plaintext changed (thanks to property n°3) and gather info on the length of the prefix.

I can illustrate all these points with one diagram. Take some time to review it and continue reading the explanation below.

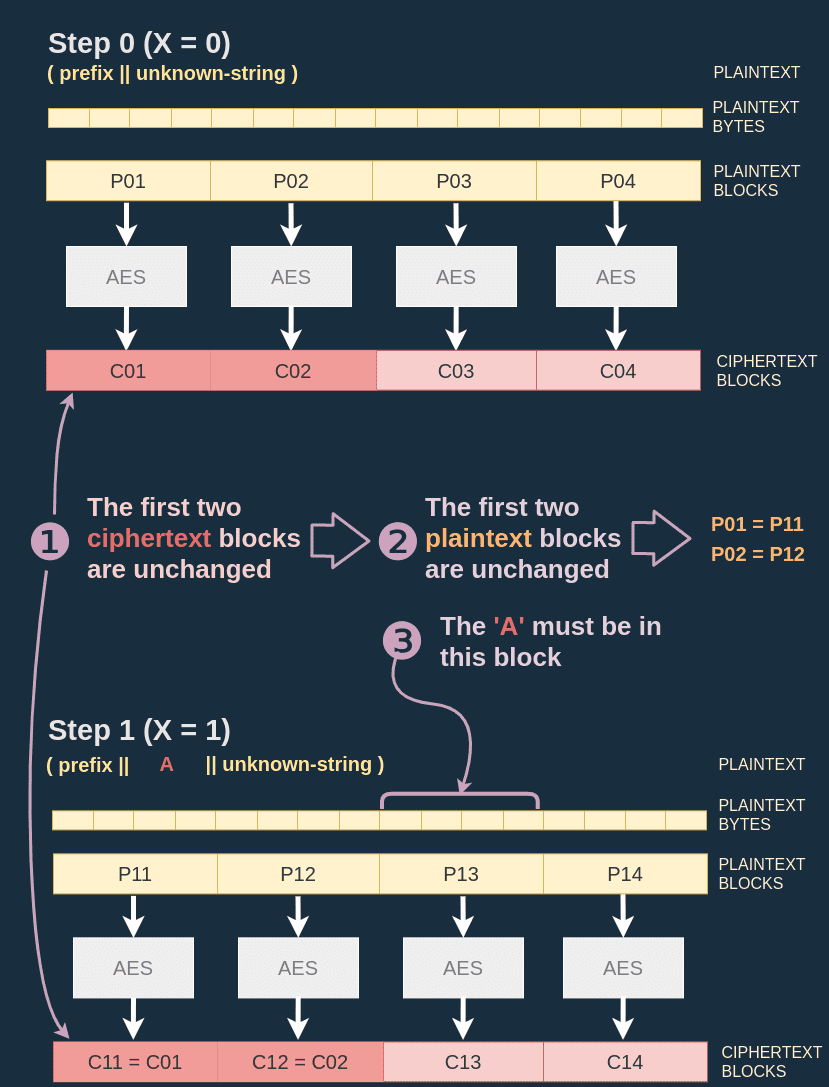
In the diagram above I set X = 0 (empty message) so that the oracle generates the plaintext P0 = (prefix || unknown-string), then I retrieve the result of the encryption C0. I do the same for X = 1, the plaintext P1 is equal to (prefix | 'A' | unknown-string).

According to point 2. since I inserted the letter A in the plaintext, I must have modified the block where the A was inserted and every subsquent block.

When looking at the blocks I can observe that C01 and C02, the first two blocks of C0 are equal to C11 and C12, the first two blocks of C1. According to point 3. this means that first two blocks of P0 and P1 are equal. This means that my letter 'A' must have been inserted in the third block of P1.

Since the letter A is added just after the last byte of the prefix I can draw the conclusion that the prefix is at least taking the first two blocks (so 8 bytes) and might be taking part of a third block (but not all of it). I just gathered the following information on the prefix size:

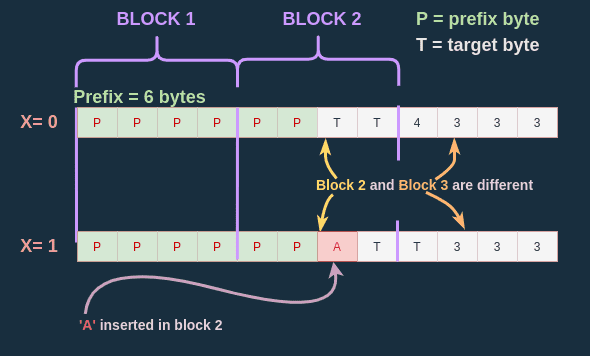
To effectively compute the prefix size I have to add a fifth observation to the four previous ones.

5. For each message of length $X \ge \text{Block Size} -1$, the blocks containing a prefix byte will never change.

Assuming that $L = 1$, the prefix is one byte long, the block size is 4 bytes long, so once I have added 3 bytes A I have "filled" the block containing the prefix. So for every $X \ge 3$, the first block will remain unchanged.

How does this help ? Well it limits the scope of my search ! I know I don't need to vary my X further than Block size - 1.

Determining the prefix size

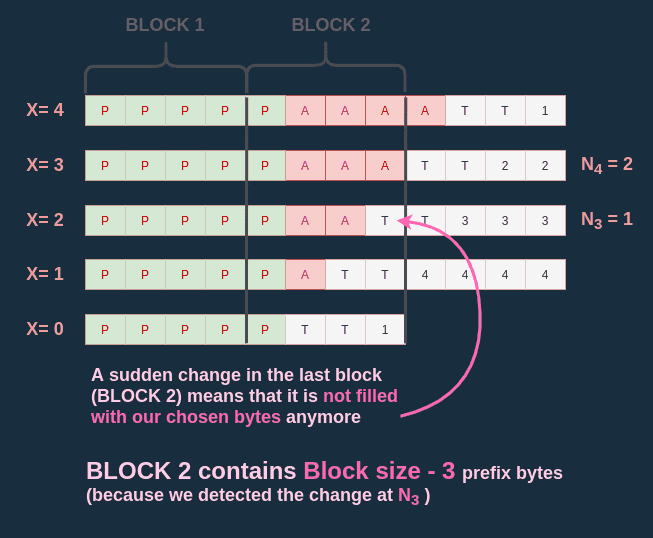
Here is my idea to find the prefix length $L$. I start with the biggest $X$ I can, this would be $\text{Block size}$ (X=4). This gives me the ciphertext C. I do this because by starting with a message the length of a block size I know that:

1. the last block of the prefix is filled with my message bytes
2. I have at least one message byte overlapping on the next block (not containing any prefix byte)
3. So if I decrement $X$ I'll still have the last block of the prefix filled with my message bytes

Then I decrement $X$ by $1$ (X=3) and count the number of subsequent blocks that stayed the same with C. With my block size equal to 4, I note this value $N_4$.

I continue by decrementing $X$ by $1$ (X=2) and count the number of subsquent blocks that stayed the same with C. I note this value $N_3$.

• If $N_4 = N_3$ then I know that I haven't changed the last block of the prefix. This means that the prefix has at least $2$ bytes in the last block and I should continue the process by decrementing $X$.
• If $N_4 \neq N_3$ then by removing one byte of my message I have changed the last block of the prefix. This must mean that in the previous state, my message was completely filling the last block of the prefix. Which in turn means that the last block of the prefix was composed of $\text{Block size} - 3$ bytes of prefix.

If this isn't clear, I hope this diagram can help:

Edge case

There is one case I haven't approached in my demonstration: when $L$ is a multiple of the block size. This happens when we reach X=0 in our algorithm but never detected a change in any $N_i$.

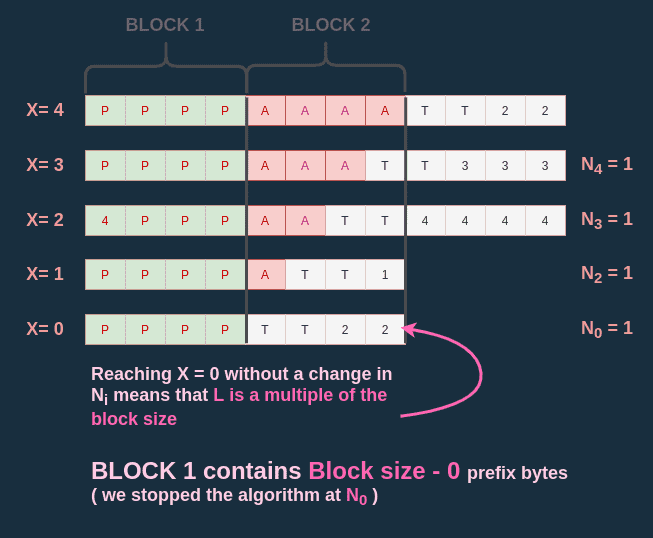
Algorithm to find the prefix size

// Max number of blocks unchanged
let Nmax = 0
// Step counter
let i = 4
// Cipher computed in step i
let cipher = oracle('A'*i)

// Algorithm
do {
  i--
  // New cipher
  newCipher = oracle('A'*i)
  // New number of blocks unchanged
  Ni = countCommonSubsequentBlocks(cipher, newCipher)
  // Initialization for 1st round
  if Nmax == 0 {
    Nmax = Ni
  }
} while (i > 0 && Ni >= Nmax)

// Edge case
if Ni == Nmax {
  L = Nmax * 4 - i
} else {
  // (i+1) is the number of bytes of the payload used
  // to "fill" the last block of the prefix
  L = Nmax * 4 - (i + 1)
}

Decrypting the unknown string

It turns out that finding the length of the prefix was the hardest part of the challenge. Now that I have this information, I can find the length of the unknown string and reuse the principles of the Challenge 12 to decrypt it, one byte at a time. I just have to slightly adapt my code to take into account the shift created by the prefix.