Cryptopals - Detect AES in ECB mode
In the eleventh challenge of the Cryptopals crypto challenges, a file containing hex-encoded ciphertexts is given:
8a10247f90d0a05538888ad6205882196f5f6d05c21ec8[...]
bd20aad820c9e387ea57408566e5844c1e470e9d6fbbdb[...]
ed9eccbe79394ca0575a81d1fa51443aa3e83e5e3cdb7a[...]
...One of these ciphertexts was encrypted with AES-ECB, the goal is to find which one.
This article is high level, to find the code take a look at my repository
AES-ECB
ECB (Electronic Codebook) is the most basic mode of AES. It can be explained in two steps:
- Step 1: the plaintext is divided in blocks of 16 bytes
- Step 2: each plaintext block is encrypted to produce the ciphertext blocks :
The problem with ECB mode is that two identical plaintext blocks will produce the same ciphertext blocks. The following string will have 4 plaintext blocks, two of which will be equal to "intelligence is" :
The two identical plaintext blocks produce two identical ciphertext blocks :
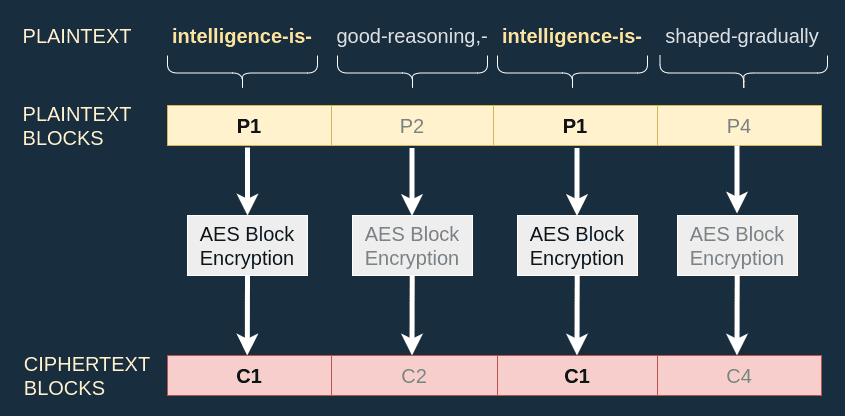
AES-ECB detection
This specificity can help identify if a ciphertext was encrypted with AES-ECB.
- First I divide the ciphertext in blocks of 16 bytes:
- Then I count the number of times each block is repeated (with a hashmap):
| Ciphertext block | Count |
|---|---|
| C1 | 2 |
| C2 | 1 |
| C3 | 3 |
| ... | ... |
If more than one block is repeated, I can consider that the oracle is using AES-ECB (and this strategy works for the challenge).
Collision probability
In the challenge the ciphertext is composed of 321 bytes, which corresponds to 20 blocks. If the ciphertext is longer shouldn't there be some natural occurence of ciphertext block repetition ? This leads to two important questions:
- What is the probability that two blocks collide according to the number of blocks in the plaintext ?
- What is the number of blocks necessary to have ?
The questions I am aksing myself are directly related to the birthday paradox. I can use the equations solving this problem to solve mine.
🥳 Birthday paradox
In a set of people, what is the probability that two of them share the same birthday ? You'll find that if we have .
This means that with only 23 random people and 365 birthdays, there is more than 50% chance that at least two of them share the same birthday! This counter-intuitive result gave the problem its designation of "paradox".
If is the set of all possible blocks, the number of blocks then the equation is:
Note that a block is made up of 128 bits so there are possible blocks. The equation above can be tricky to apply in the real world so we use an approximation:
In our case .
There is also an equation to compute the number of elements required to get a certain probability:
We have . This means that when our ciphertext is composed of approximately blocks, we have a 50% chance of having a collision.
Conclusion
To detect if AES-ECB was used, check if two blocks in the ciphertextext collide. As long as the ciphertext contains less than blocks, this should work properly.
Check out my other articles about the Cryptopals challenges!