Cryptopals - CBC bitflipping attacks

Premises

In challenge 16 of the Cryptopals challenges I am given an oracle very similar to the one in Challenge 13.

The goal of the challenge is to modify a ciphertext encrypted with CBC so that the decrypted plaintext will contain the string ;admin=true.

Then encryption function:

1. Takes a string as its input and quotes the ";" and "=" characters.
2. Prepends the string with "comment1=cooking%20MCs;userdata=".
3. Appends the string with ";comment2=%20like%20a%20pound%20of%20bacon".
4. Encrypts the string with AES-CBC.

Oracle(message) = AES-128-CBC(prefix || sanitize(message) || suffix)

AES-CBC reminder

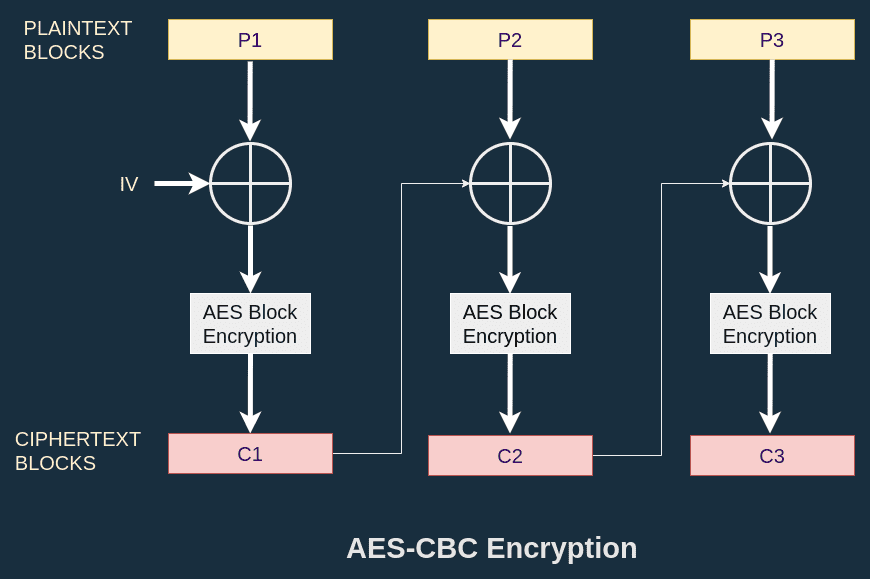
A good understanding of how AES-CBC works is necessary to find out how to solve the puzzle.

AES-CBC (Cipher Block Chaining) mixes the previous ciphertext block with the new plaintext block before applying the AES block encryption. For the very first block, AES relies on an Initialization vector noted IV. This IV is not secret but should be random. There are two interesting properties here:

• Unlike with ECB mode, each ciphertext depends on the whole previous chain of ciphertexts.
• A plaintext block will not produce the same ciphertext block twice because it is mixed with something else before.

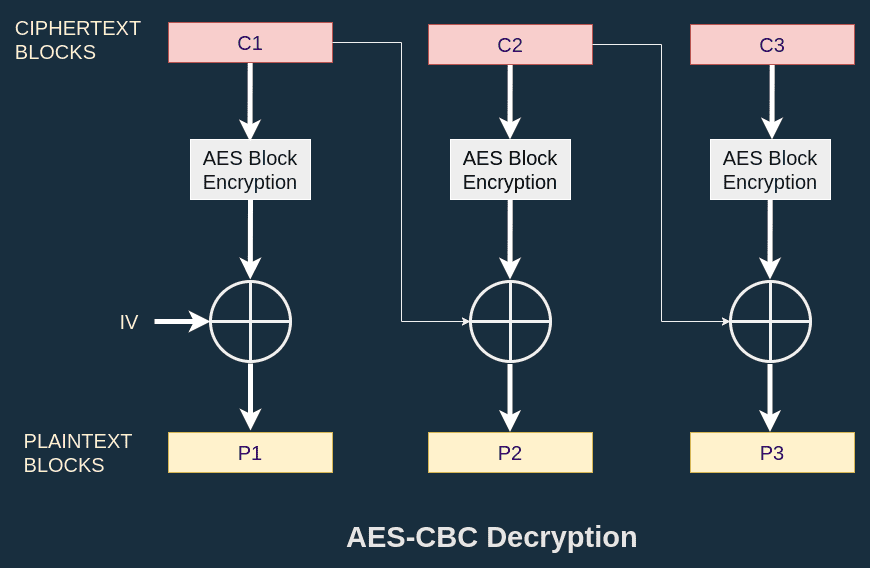
The decryption is the same graph, but mirrored:

Known values and levers

My goal is to modify the ciphertext so that the decryption contains the string ;admin=true. It turns out that this string is 12 bytes, which fits in a 16 bytes block. So I just have to modify one ciphertext block to make it contain my target string. I call $\text{Pt}$ the target plaintext produced by the modified ciphertext block.

During the decryption process, there are some values that I know. In the diagram below, I show that I know the AES block decryption of $C1$:

I note this value $\text{I1}$.

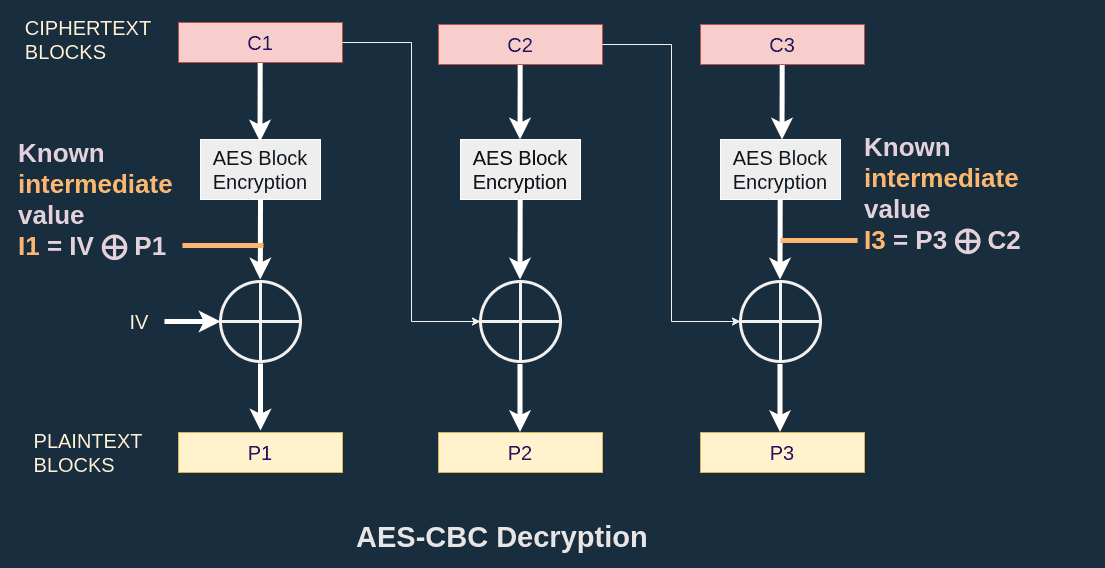
Since I know $\text{I1}$, I target a specific $\text{Pt}$ and I have control over the ciphertext and the IV, I just have to apply some basic maths to solve my problem. I can compute a new initialization vector $\text{IV'}$ such that the plaintext produced is $\text{Pt}$

There nothing more to it. Check out my Github repository to find the full code solving this challenge.